Labeled PSI from Homomorphic Encryption with Reduced Computation and Communication

发表于 更新于 分类于

以减少计算和通信的方式从同态加密中获得标记的 PSI

众所周知，完全同态加密（FHE）可用于在不平衡设置中建立高效的（标记的）隐私集合求交协议，其中一个集比另一个大得多（Chen 等人（CCS'17，CCS'18））。在本文中，我们展示了对这些工作的多种算法改进。特别是，我们的协议有一个渐进的更好的计算成本，只需要 同态乘法，并且通信复杂度在较大的集合大小 中是亚线性的。

我们证明我们的协议在许多实际参数上明显优于 Chen 等人（CCS'18）的协议，特别是在在线通信成本方面。例如，当相交于 和 个项目集时，我们的协议减少了 71% 以上的在线计算时间和 63% 以上的通信。当相交于 个和 个项目集时，我们的协议将在线计算时间减少 27%，通信减少 63%。我们与其他最先进的不平衡 PSI 协议的比较表明，当 时，我们的协议具有最佳的总通信复杂度。对于有标签的 PSI，我们的协议也优于 Chen 等人（CCS'18）。当相交于 和 个项目集时，较大的项目集有相关的 字节的标签，我们的协议将在线计算时间减少 67% 以上，通信减少 34%。

最后，我们展示了一种修改，在更大的集合规模 下，通信成本几乎不变，但在今天的 CPU 上计算复杂度高得不切实际。例如，要使一个 项的集合与 、 或 大小的集合相交，我们的概念验证实现只需要 0.76MB 的在线通信，这比 Chen 等人（CCS'18）的改进超过了 24 倍。

1 介绍

考虑到两方，每一方都有一个隐私的项目数据集。他们想在不向对方泄露任何其他信息的情况下了解各自数据集的交集。例如，两个国家希望通过在其警察数据库中找到匹配的身份来追踪犯罪嫌疑人，同时向对方隐藏其他敏感数据，或者两家银行希望识别有不明显的金融交易的客户，而不透露关于客户的任何其他数据。

为了解决上述问题，双方可以进行隐私集合求交（PSI）协议。PSI 指的是一种交互式加密协议，它将两个隐私集合作为输入，找到它们的交集，并将其输出给参与者中的一方或双方。如果一方获得 PSI 协议的结果（单向 PSI），我们称这一方为接收方，另一方为发送方。一般的双向 PSI 可以通过两轮单向 PSI 来实现，其中参与者互换接收方和发送方的角色。在实践中，单向 PSI 在各种隐私保护协议中作为一个重要的基本要素而存在，包括移动信使（如 Signal 或 WhatsApp）中的隐私联系人发现 [28, 42]，检查漏洞数据库中是否存在泄露的密码 [2, 37]，以及用于控制传染病传播的联系人追踪 [60]。

在这项工作中，我们专注于单向 PSI 的一个变体，其中接收方的集合比发送方的小得多。我们还假设接收方的计算和存储资源有限（例如，手机或可穿戴设备），而发送方配备了更强大的机器（例如，数据中心的服务器）。这种特定的设置被称为不平衡的。因此，不平衡的设置的目标是将尽可能多的计算委托给发送方，并减少双方的通信。

令 和 分别表示发送方和接收方的集合；在不平衡的 PSI 中，我们有 。目前最先进的非平衡 PSI 协议具有 通信成本 [36] 或 计算复杂性 [13]。我们将专注于后者的工作，它可以实现准对数的通信复杂性。我们的工作使用 ，即允许在加密域的任何固定乘法深度的算术电路上进行计算，而不需要解密的随机加密。诸如 BGV [7] 和 BFV [22] 这样的 方案在通信和计算复杂度方面都引起了与乘法深度有关的类多项式的开销。

按照 [13] 的大纲，我们还考虑了标签化的 PSI，这是一种特殊类型的带计算的 PSI。在这种情况下，发送方集合中的每个元素都有相关的数据标签，而接收方希望了解交集中的元素的标签。这是由 Chor 等人 [16] 介绍的单服务器隐私信息检索（PIR）问题的一般化。标签化 PSI 的实际应用包括有针对性的价格歧视 [45] 和移动信使中的密钥检索 [28, 42]，其中用户查询其联系人列表中的人的公钥。

1.1 相关工作

20 世纪 80 年代的早期 PSI 协议 [33，43] 是基于 DiffieHellman（DH）密钥交换的 [18]。从本质上讲，Alice 和 Bob 对他们集合中的每一个元素进行 DH 密钥交换；如果产生的共享秘密相匹配，就会发现匹配。Freedman 等人 [24] 介绍了一个基于不经意多项式评估和同态加密的协议。Ateniese 等人 [4] 介绍了一种基于 RSA 累加器的结构。由于 PSI 可以被认为是安全两方计算的一个特例，因此可以使用标准技术，如混淆电路来构建 PSI 协议 [32, 49, 51]。最近，许多协议 [12, 19, 40, 46, 48, 52, 55] 都是基于 OT 扩展 [34] 和不经意伪随机函数（OPRF）。

上述工作主要是为平衡设置而设计的，其中发送方集与接收方集大致相同。下面我们将放大文献中的两个最有效的非平衡设置的范式，这也是本工作的重点。

1.1.1 基于 OPRF 的不平衡 PSI

一个基于 OPRF 的 PSI 协议首次在 [23] 中提出，其中 OPRF 是由 Naor-Reingold（NR）伪随机函数 [44] 构建的。在混淆电路（GC）[61] 的帮助下，后来的工作从基于 AES 的 OPRF [50] 引入了一个 PSI 协议。目前最先进的协议在 Kales 等人 [36] 的工作中实现，它来自 [39] 和 [54]。该协议有两个阶段，预处理阶段和在线阶段。作者引入了许多优化，将尽可能多的计算和通信成本推到预处理阶段。下面我们对这一思路的协议思想进行概述。在预处理阶段，具有大集合 的发送方产生一个 密钥 ，并对每个 计算 。然后，它将每个 输出插入一个布谷鸟过滤器 [21]，并将其发送给接收器。为了计算在线阶段的交集，接收方在发送方的帮助下计算 。也就是说，接收方在不知道 的情况下，为其集合 中的每一个值 获得 。最后，接收方在本地检查其任何项目是否在布谷鸟过滤器中。

在线阶段是非常有效的，并且不依赖于发送方的集合大小。对于一个有 个项目的接收器，通信开销只比 2 兆字节高一点 [36]。由于使用 GC 版协议时没有昂贵的公钥操作，所以计算也很高效。这类协议的最大瓶颈是预处理阶段的带宽消耗和存储需求。也就是说，发送方必须分发给每个接收方的布谷鸟过滤器与发送方集合的大小是线性关系。当发送方集合有 个项目时，布谷鸟过滤器的大小超过一千兆字节 [36]。

1.1.2 基于 FHE 的不平衡 PSI

在光谱的另一边，Chen 等人 [14] 引入了一个基于 的非平衡 PSI 协议，该协议的通信开销在（较小的）接收方集合中是线性的，在（较大的）发送方集合中是对数的。他们的工作后来在 [13] 中得到完善，该协议使用 OPRF 加强了安全模型，允许任意长度的项目，并将该协议扩展到具有任意长度标签的 PSI 设置。

在这两项工作 [13, 14] 中，都使用了 BFV 方案 [22]，它有 内存和 运行时间开销，其中 是计算的乘法深度。PSI 协议的通信成本是 密文，其计算复杂性是 同态乘法，乘法深度 。因此，对发送方集合大小的依赖性被量化为：通信复杂度为 ， ，而计算复杂度为 。

该工作原理是这项工作的起点。因此，我们将详细解释推迟到第三节。

1.2 贡献

我们对 Chen 等人 [13, 14] 的协议进行了一些优化和改进，从而改善了运行时间，并提高了发送方集合大小的通信复杂性。我们的贡献可以总结为以下几点。

  • 我们展示了如何去除 [13] 中使用的缓慢的扩展场算术，同时仍然支持任意长度的项目和标签。
  • 我们通过使用极端邮票基数 [11] 而不是 [13, 14] 中效率较低的窗口技术来降低通信成本。
  • 我们展示了如何使用 Paterson-Stockmeyer 算法 [47] 在 密文间乘法中评估交叉电路，这比 [13] 有了四倍的改进。
  • 我们使用 [56] 的技术来实现 FourQ 曲线 [17] 的一个非常快速的哈希曲线的实现。基于 OMGDH 的 OPRF 协议 [13, 35, 54] 需要哈希到曲线，这是我们协议的一个关键组成部分。
  • S 我们通过利用无深度的同态 Frobenius 自动化来改善通信开销。这种操作允许计算 ，其中 是 FHE 方案的明文模数，而不需要密文间乘法。因此，为了计算深度为 的交叉电路，发送方只需要 个密文。这将通信复杂度从先前工作 [13, 14] 中给出的 降低到了 ，其中 。
  • 我们创建了一个我们协议的开源参考实现。

2 初步了解

2.1 符号

在本文中，我们用 表示整数 的集合， 是对 情况的缩写。以 为底的对数用 表示。对于 的二进制对数，我们省略基数，写成 。矢量用带箭头的小写拉丁字母表示，即： 。对于一个给定的向量 ，其 1 范数定义为 。

2.2 不平衡的 PSI

有接收方和发送方，两方分别拥有一个集合 和一个集合 ，。我们假设 ，并且集合的大小是公开的。每个集合包含一对字符串 ，其中 是一个元素 ID， 是其标签。ID 的长度 和标签的长度 在 的所有元素中共享。 一个（单向）PSI 协议是一个交互式协议，它向接收方输出 ，而向发送方不泄露任何关于 和 的其他信息。在标签化 PSI 中，协议将 返回给接收方。

2.3 全同态加密

全同态加密（FHE）是一个加密方案系列，允许在不解密的情况下对加密数据进行任意操作。大多数现有的 FHE 方案 [69, 15, 20, 22, 25, 27] 是基于 LWE [53] 或 RLWE [41] 问题，这意味着加密信息中存在噪音。与密码文本相关的噪声随着每次同态操作的进行而增长（加法是加法增长，乘法是乘法增长）。因此，为了避免解密错误，我们必须注意确保噪音不会大到足以干扰基础明文。这种噪音管理是通过两个框架实现的。

第一个框架包括一个有限同态加密（somewhat homomorphic encryption, SHE）方案，它能够同态计算自己的解密电路，或者执行一个所谓的引导操作，减少噪音大小。对于这样的 FHE 方案，加密参数可以被固定，以便在给定引导信息的情况下，任何电路都可以计算。然而，与其他同态操作相比，引导操作要慢得多；因此，在实践中通常会避免这种操作。

第二个框架的想法是选择足够大的加密参数来计算一个预先确定的电路系列。在这种情况下，从来没有使用引导，但加密参数随着电路的深度而增长。其加密参数随着电路深度的增加而呈多项式增长的 SHE 方案被称为 方案。对于足够浅的电路， 方案在实践中更有效率。

在这项工作中，我们使用了两个 方案，BGV [7] 和 BFV [22]，分别在 HElib [31] 和 SEAL [57] 库中实现。这两种方案都是在环 上定义的，其中 是阶为 ，度为 的循环多项式。他们的密文空间是 ，其中 是一个正整数。每个密文的大小为 。

这些方案的明文空间被类比定义为 ，用于某个正整数 。每个明文的大小为 。我们假设 是一个素数。让 成为 的乘法顺序。在这种情况下， 分裂为 个度为 的因子。因此，中国余数定理产生了同构的 。 的每个副本被称为槽。利用这种同构性，我们可以将 中的多个数据值编码并加密成一个密码文本，并使 上的同构加法和乘法对应于编码值上的槽式加法和乘法。这样的编码被称为 SIMD 打包 [59]。滥用符号，我们用 ⟦⟧ 来表示在其一个槽中加密一个值 的密文。

噪声大小由噪声分布的标准偏差 定义，通常设置为 。

参数 、 和 定义了我们方案的安全级别，其中 表示噪声分布的标准偏差，通常设置为 。安全级别是用 LWE 估计器 [1] 估计的。

同态操作及其成本：我们使用的基本同态运算是加法和乘法，它们可以在两个密文或由密文和明文组成的组元上进行。我们还将使用 Frobenius 运算，给定一个加密信息 ⟦⟧ 和一个正整数 ，返回 ⟦⟧ （更多细节见 [26]）。

每个同态操作的成本由其运行时间和添加到其输出的噪声量定义。对于成本分析，我们假设密文和明文都以 Double-CRT 形式表示 [26]，密文的噪声以其无穷大规范来衡量。我们还假设使用混合密钥切换方法（更多细节见 [38]）。

同态加法是最后一个昂贵的操作，只需要 个整数加法。输出噪声是输入噪声的总和，大约是 的一个小系数。

明文与密文的乘法，我们称之为标量乘法，相当于 维的向量的 系数乘法。因此，这个操作需要 个整数乘法。标量乘法将输入的噪声按 的系数进行缩放。

密文与密文的非标量乘法有两个步骤：向量卷积和密钥切换。第一步执行 个整数乘法，第二步执行 个整数乘法。因此，非标量乘法的运行时间是 个整数乘法（见 [38]）。如果输入的密码文本有大小为 和 的噪声，那么它们的乘积的噪声就等于 。

Frobenius 操作首先对密码文本的 Double-CRT 形式进行置换，然后进行密钥切换。置换不需要整数乘法。因此，Frobenius 操作比非标量乘法更快，其运行时间被密钥切换所支配；它需要 整数乘法。Frobenius 运算引入的噪声也被密钥切换引入的噪声所支配（见，例如，[29]），它为输入密文增加了大约 的噪声。

总而言之，无论是在运行时间还是在噪声增长方面，最昂贵的同态操作都是非标量乘法。因此，我们用非标量乘法的数量来衡量我们算法的运行时间复杂性。我们还衡量了我们的电路与非标量乘法有关的深度。那么，我们说，一个（顺序的）非标量乘法会消耗一个乘法层次。

请注意，在计算密文的平方时，非标量乘法有时可以用 Frobenius 运算代替。由于 Frobenius 运算只引入了加性噪声，我们说 Frobenius 运算不消耗任何乘法等级，也就是说，它是无深度的。

3 不带标签的 PSI

我们的基本 PSI 协议严格遵循 Chen 等人 [13, 14] 的框架，这些框架是基于 [49] 的想法。

输入: 接收者有一个大小为 的输入集 。发送方的输入是一个大小为 的集合 。两个集合都包含长度为 的比特串。 , 和 的值是公开的。

输出: 接收者输出 。

设置: 接收方和发送方商定一个 SHE 方案，明文空间是一个有限域 。他们还公开选择哈希函数的数量（通常是三个） , 其中 是一个正整数。最后，他们商定一个 函数 。

接收方生成 SHE 方案的公钥和私钥。发送方对 密钥 进行采样，并计算 。然后，双方交互，将 应用于接收方的集合，由此接收方得到 。现在计算𝑋 ∩ 𝑌相当于计算 。

我们注意到，使用 值而不是原始值有多种好处。最重要的是，有必要提供针对恶意接收者的安全性，因为同态加密不会自动为发送者的输入提供输入隐私。为了解决这个问题，[14] 使用噪声淹没技术来证明针对半诚实的接收者的安全性，但他们的方法并没有扩展到恶意的情况。另一个原因在下面第 3.1 节有更多的讨论：使用 值可以让我们完全避免昂贵的扩展字段算术。

接下来，接收方将每个 放入布谷鸟哈希表 ，仓的大小为 。具体来说，它将构建一个表 ，使得 中的仓没有一个以上的元素，并且对于所有的 都有一个 ，使得 。发送方创建了一个布谷鸟哈希表 ，其 |𝑋 | ≫𝑀大小可能大于 。对于所有的 和所有的 ，发送者将 放入 ，同样，允许每个仓有多个 。[14] 中显示，如果 ，那么发送方的每个仓包含 个值的概率很大。这种设置保证了 和 的交集等于各自的仓交集的联合，即： 其中 表示在 处的 值。双方将各自的仓编码到明文字段 中，接收方将其所有仓加密并发送给发送方。

交集: 给出仓 的加密 ⟦⟧ ，发送方计算出交集多项式： ⟦⟧⟦⟧⟦⟧ 如果 ，则 ⟦⟧ 是对 的加密。否则， ⟦⟧ 就会对 中的某个非零值进行加密，这取决于 。这个非零值不会泄露任何关于 的信息，因为有 步骤。发送方将 ⟦⟧ 发送给接收方，接收方对其进行解密并检查 是否等于 。

安全性: 如 [13] 所示， 步骤使上述 PSI 协议在随机预言机模型中对恶意接收者是安全的，并对恶意发送者提供隐私。我们的协议在算法方面与 [13] 不同；安全保证和安全证明与 [13] 相同，即该协议保证对恶意接收者的安全和对恶意发送者的隐私 [30]。如 [13] 所述，只要有少量额外的计算开销，该协议就可以升级，以提供对恶意发件人的进一步保护。

3.1 优化

在这一节中，我们讨论了各种优化技术，以使上述协议实用。其中一些（SIMD 打包、分割和分窗）在过去的 [13, 14] 中已经讨论过了，并且对我们的协议仍然至关重要。我们改进了 SIMD 打包技术，只使用更有效和更灵活的素数域，尽管这主要是在下面第 4 节讨论的标记情况下提出的挑战。我们利用 Paterson-Stockmeyer 算法 [47] 来提高计算复杂性，并实现新的通信 - 计算权衡。我们改变了开窗技术，使用更有效的极端邮票基数 [10, 11]，这在许多情况下大大降低了我们的通信成本。我们展示了可以用零乘法深度计算接收器输入的多少个幂，从而产生了一个通信成本极低的协议变体。最后，我们为 FourQ 椭圆曲线 [17] 改编了 Elligator 2 [5] 图，以实现快速哈希到曲线，这是基于 的 协议所需要的。

基于交换的散列 [49] 可以在我们的工作中立即应用，以减少项目长度的几个比特。但是，与我们的其他技术相比，这种技术对性能的影响微乎其微，所以我们没有把它纳入这项工作。

3.1.1 SIMD 打包

正如第 2.3 节所讨论的，我们可以将多个数据值打包到一个密文中，这样这些值就可以同时被同态操作处理。使用这种方法，接收方基本上可以把密文中的槽当作布谷鸟哈希表 的仓，从而把多个值 编码在一个密文中。发送者随后可以并行计算几个交叉电路（公式（1）），这使得计算和通信成本都有了明显的改善。

在 [13] 中，作者能够支持任意长度的项目，首先将它们散列到一个较小的域中，并使用 SIMD 打包，扩展字段的值大到足以容纳哈希值。不幸的是，扩展字段运算会对性能产生破坏性的影响；这种影响在标签模式下尤为突出。此外，扩展字段必须具有一定的大小特征才能发挥作用，这在某些情况下会导致次优的参数选择。

我们观察到，完全不使用扩展字段是可能的，而只在素数域上使用 SIMD 打包。由于元素哈希值大于一个 SIMD 槽，我们简单地将哈希值拆分，以占据几个连续的槽。这在 [13] 中是不可能的，因为作者认为 步骤是可选的：由于单个 SIMD 槽的值很小，它们可以被猜到，甚至一个半诚实的对手可以以不可忽略的概率了解部分匹配项目的信息。这个问题通过始终执行 步骤来解决，该步骤将项目随机化并保护发送者的数据集不被部分项目泄露。在有标签的情况下还有一些问题，我们将在第 4 节讨论和解决。

3.1.2 分割

为了减少计算深度，[14] 提出将每个发送者的仓分成 个子集，然后分别计算这些子集的交集。如果 是一个发送者的仓的最大尺寸，那么这种方法将电路深度从 减少到 ，代价是发送者发送给接收者的密文数量增加 倍。

为了计算度数为 的相交多项式 ⟦⟧ ，发送方可以首先计算所有的单项式幂 ⟦⟧⟦⟧ 使用 非标量乘法。这些幂可以重复使用，以计算每个 分区的相交电路。分区的另一个好处是：在单项式幂被计算过一次后，它们可以被用于每个分区，即计算 次，以相对便宜的标量乘法运算来评估相交电路。

3.1.3 Paterson-Stockmeyer 算法

分区的一个问题是，在许多情况下，把 看作是相对较大的（比如，几千），需要 的非标量乘法，而 保持相对较小（比如，10）是有利的。在这种情况下，非标量乘法的计算成本可能主导了在线运行时间。我们建议应用 Paterson-Stockmeyer 算法 [47] 来计算 非标量乘法中的相交多项式。现在我们解释一下这个算法的原理。

首先，挑选正整数 和 ，使 ，且 。发送方开始计算接收者的密文 ⟦⟧ 的低次幂 ⟦⟧⟦⟧⟦⟧ 和高次幂 ⟦⟧⟦⟧⟦⟧⟦⟧ 。那么求交多项式可以改写为： ⟦⟧⟦⟧⟦⟧ 其中， 是 的第 个系数。内部和可以通过标量乘法和加法从低次幂计算出来。非标量乘法只需要将这些内部和乘以高次幂。计算 ⟦⟧ 的总计算复杂性等于： 非标量乘法。当 时，达到最小的非标量复杂性 。

事实上，Paterson 和 Stockmeyer 设计了一个稍快的算法，具有相同的渐近复杂度。不幸的是，在我们的工作中不能直接利用它，因为它依赖于这样一个事实：被评估的多项式的系数环是一个欧几里得域。 ⟦⟧ 的系数是来自环 的明文，它不是欧几里得的。

如果使用分区技术，那么 ⟦⟧ 被 多项式 ⟦⟧ 取代，度为 的 。选择正整数 ， ，使 ＝ 。为了评估每个 ，发送方预先计算 低次幂和 高次幂，并按公式（2）计算每个 。对每个 进行高次幂乘法，即 次。这意味着评估每个 的非标量乘法复杂性等于： 与公式 (3) 类似，最小的非标量复杂度 是通过取 来实现的。

例 1. 考虑一个大小为 的仓。根据分区的数量 ，我们可以用 Paterson-Stockmeyer 方法或朴素方法来计算交集，即预先计算所有的幂 ⟦⟧⟦⟧ . 当 时，Paterson-Stockmeyer 方法需要较少的非标量乘法，如下表所示：

image-20220802215601146

在附录 A 中，我们展示了如何从 和 中识别出带有分区的 Paterson-Stockmeyer 方法是否优于朴素的方法。

3.1.4 分窗

在现代的 方案中，加密参数的设置取决于计算的乘法深度：更高的乘法深度需要更大的参数。不幸的是，较大的参数会增加通信和计算的复杂性。

Paterson-Stockmeyer 算法的乘法深度（如公式（2））等于 ，这最多比计算程度为 的多项式的深度大一个。为了减少深度，接收方可以发送额外的预计算的 幂的加密。例如，如果 ⟦⟧ 和⟦⟧ 给了发送方，它可以用深度为 的电路计算公式（2）。由于当 时，乘法复杂性最小（公式 (3)），计算交集多项式 (2) 的深度等于： 发送更多的额外幂，减少了乘法深度。如 [14] 所述，窗口技术依赖于这样一个事实：任何整数 都可以在某个基数 中唯一地表示，即 ， 。这意味着。如果所有幂 ， 和 是预先计算的，那么 可以通过深度为 的电路获得。因此，接收方可以发送这些 额外幂的加密，这样，发送方可以计算所有幂⟦⟧⟦⟧，具有上述深度。

在实践中，固定一个乘法深度 并从中推导出 是很方便的。由于函数 随 增加，支持深度 的最小可能的 导致从接收方发送到发送方的密文数量最少。

让 成为目标深度。这意味着， 应该满足： 因此，我们得到 ，因此 。因此， 是满足 的最小整数，或者说 。因此，必须发送的幂数量被限定为： 在使用 Paterson-Stockmeyer 算法时，发送方应计算低次幂和高次幂，然后用低次幂的线性组合乘以高次幂，如公式（2）。这意味着，为了在计算相交多项式时达到目标深度 ，发送方应该能够以最多 的深度计算两组幂。

按照上面的讨论。我们得到，接收方应发送 的加密的 个幂，以便发送方基于 计算低次幂。为了计算具有相同深度的高次幂，发送方只需要 对 的幂进行加密，基数 。接收方需要发送的幂数的上界由以下定理定义。

定理 2：要用 Paterson-Stockmeyer 方法计算一个度数为 、乘法深度为 的多项式⟦⟧，发送方需要少于 个 ⟦⟧ 的幂。

证明可以在附录 B 中找到。

3.1.5 极值邮票基 (Extremal postage-stamp bases)

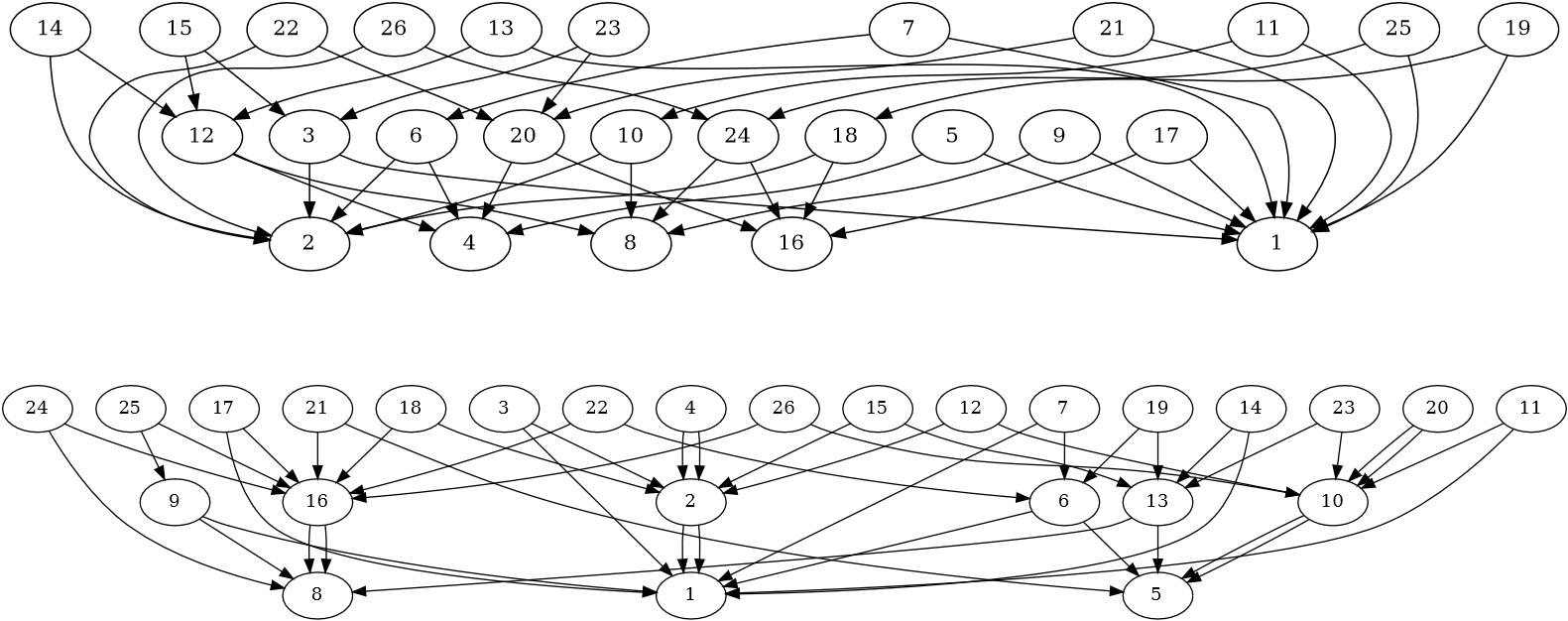
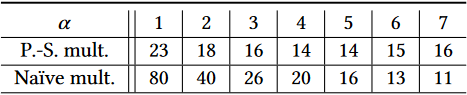
上面描述的 [14] 的窗口技术很容易使用：接收器总是确切地知道要发送哪些幂。不幸的是，它远非最优。为了证明这一点，考虑一个 的情况。用户可以选择加密并发送他们查询的幂 ，发送方可以用这些幂在深度二计算中计算出 以内的所有幂，如图 1 的第一个图形所示。然而，图 1 的第二个图展示了另一种计算，也是深度二，但只有三个源幂： . 这立即转化为接收方到发送方的通信量减少了 40%。

image-20220802222612515

图 1：图中描述了发送方从一组给定的源幂中计算出接收方查询的所有幂至 26 的两种可能方式。从一个节点上伸出的两个箭头表示哪些较低的幂需要相乘，以产生节点标签中所示的幂。

更一般地说，我们想回答的问题是：应该发送哪些查询的幂，以便发送者能够计算查询的所有幂，直到尽可能大的边界 ，而不超过一个目标深度。

这个问题可以被看作是全球邮戳问题的一个变种 [10, 11]。

定义 3（全球邮票问题）：给定正整数 和 ，确定一组 个正整数 ，使得所有整数 可以写成 或更少的 之和，并且 尽可能大。 集被称为极值邮票基。

与我们的问题的联系是明确的。在定义 3 的符号中，如果接收方将加密的幂 ⟦⟧⟦⟧⟦⟧ 发送给发送方，那么发送方可以在乘法深度 计算所有幂到 。具体来说，考虑图 1 中使用的幂 。在收到 ⟦⟧⟦⟧⟦⟧ 后，发送方在所有整数上（按顺序）迭代到 ，对于它尚未计算（或收到）的每个幂，它选择一种深度最优的方式来计算它作为两个低次幂的积。这正是图 1 中的图形是如何产生的。事实上，基 是 , 的唯一极值邮票基 [10]。

目前还不知道寻找极值邮票基的简单方法，也不知道全局邮票问题的复杂度等级。此外，极值解往往是唯一的（或几乎是唯一的），并很快变得难以找到。幸运的是，我们只需要该问题的小实例的解决方案，这些解决方案已经被破解，并在 [11] 中提出。

极值邮票基可以通过两种方式用于 Paterson-Stockmeyer 算法。回顾一下，在这种情况下，发送方必须计算接收方查询的所有幂，直到某个正整数 ，以及所有幂是 的倍数，不超过仓的大小 。

当然，可以使用 的极值邮票基来实现第一个目标。为了使发送方能够从尽可能少的源幂中计算出尽可能多的 的幂，接收方可以应用一个（可能是不同的）极值邮票基，但这次要把指数乘以 。

例如，再次考虑图 1 中的极值邮票基 。当 时，这对 Paterson-Stockmeyer 来说非常有效。为了使用 Paterson-Stockmeyer，我们可以另外发送幂 ，这将允许服务器用深度 的电路计算高达 度的多项式。

具有大 （如 或 ）的极值邮票基可能很难找到，但如果找到了，这种基数允许在不增加深度的情况下评估非常高度的多项式，但由于需要通过非标量乘法计算大量的幂，在线计算时间可能会大幅增加。

3.1.6 通过 Frobenius 操作实现低深度指数化

如第 2.3 节所述，从运行时间和增加的噪声来看，Frobenius 运算是一种更便宜的非标量乘法的替代方法。使用这种操作，发送方可以计算 ⟦⟧ 的幂，以节省乘法深度。因此，接收方可以发送更少的幂，降低了通信的复杂性。

例 4：取一个明文模数 ；每个 SIMD 槽都与 同构，对于某个 ，Frobenius 操作可以计算 ⟦⟧⟦⟧ ，对于 。

假设发送方在其集合中有 个值。这意味着它应该计算出 度的求交多项式 ⟦⟧ 。使用 Paterson-Stockmeyer 算法，它需要 ⟦⟧ 和 ⟦⟧ 为 来计算深度为 的 ⟦⟧ ，总共，接收方必须发送 个加密这些幂的密文。

然而，发送方可以通过应用 Frobenius 运算 ⟦⟧⟦⟧ 来从 ⟦⟧ 计算出 ⟦⟧ ，这是无深度的。此外，任何偶数幂 ⟦⟧ 的奇数 都可以通过 Frobenius 运算 ⟦⟧⟦⟧ 得到。因此，接收方只需要发送 个加密幂，即 ⟦⟧ 、 ⟦⟧ 、 ⟦⟧ 、 ⟦⟧ 、 ⟦⟧ 、 ⟦⟧ 、 ⟦⟧ 和 ⟦⟧ 。有了这些次幂，发送方用 次 Frobenius 运算计算出 Paterson-Stockmeyer 算法的所有低次幂和高次幂，然后只进行 次非标量乘法，用深度 的电路计算出 ⟦⟧ 。

在增加深度的代价下，通信复杂度可以进一步降低。如果接收方只发送 ，那么发送方首先用 Frobenius 运算计算 ⟦⟧ 、 ⟦⟧ 、 ⟦⟧ 、 ⟦⟧ ，深度为 ，然后得到幂 ⟦⟧⟦⟧ ， ⟦⟧⟦⟧ ， ⟦⟧⟦⟧⟦⟧⟦⟧ ， ⟦⟧⟦⟧⟦⟧ ， ⟦⟧⟦⟧⟦⟧⟦⟧ ， ⟦⟧⟦⟧⟦⟧⟦⟧ ， ⟦⟧⟦⟧⟦⟧⟦⟧⟦⟧ ，深度最多为 的乘法二叉树回路。剩余的低次幂和高次幂再次用 Frobenius 运算来计算。因此，发送者可以计算出深度为 的 ⟦⟧ ，而只给了一个密文 ⟦⟧ 。

上面的想法在定理 5 中得到了正式体现，该定理指出了发送方用深度为 的电路可以计算出 ⟦⟧ 的多少个连续幂。这个定理意味着，如果 ⟦⟧ 的度数为 ，那么发送方只需要 个加密的 幂来计算 ⟦⟧⟦⟧ 的乘法深度为 的电路。在先前的工作 [13] 中，需要 个幂来执行相同的任务。

定理 5：令 ⟦⟧ 为加密 的明文信息的密文。令 为一个正整数。那么，使用深度 电路，发送方可以计算出所有的幂 ⟦⟧⟦⟧⟦⟧ ，其中： 本条定理的证明可以在附录 C 中找到。

例 6：令 。在这种情况下， ，所以 。由于 ，发送方可以计算 ⟦⟧⟦⟧ 的深度为 的电路，这在例 4 的第二部分中得到支持。

例 7：令 。由于 ，对于任何 ，因此 。

这种技术要求接收方发送额外的评估密钥来进行 Frobenius 操作。特别是，接收方应该向发送方发送 评价密钥，以计算幂 ⟦⟧⟦⟧ 。此外，接收方只能发送一个与基本 Frobenius 操作 ⟦⟧⟦⟧ 相对应的评估密钥。评估密钥的大小可能很大（详见第 5 节），但它们可以被发送方缓存并重复用于协议的多次执行。

在实践中，Frobenius 操作的优势与 SIMD 打包能力相矛盾。一般来说，打包能力等于 ，其中 是是明文模数 的阶数与环 的阶数 相乘，即 。这意味着 ，因此 。因此，较小的明文模数会产生较小的打包能力，但由于定 5 的存在，它的乘法深度会更好。

3.1.7 来自 FourQ 的快速 OPRF

正如第 3.1.1 节所指出的， 阶段对我们的协议至关重要。发件人的任务是很重要的：它需要选择一个随机数调制 困难群顺序作为 密钥，将其每个项目散列到一个统一的随机组元素中，并将该组元素与密钥相乘。

出于性能方面的考虑，我们使用 FourQ 曲线 [17] 作为群，它提供了随机点的快速标量乘法，以及如下的哈希到曲线的快速实现。我们应用二元映射 来修改 Elligator 2［5］的构造。对所需的 操作的朴素检查表明，这至少需要在 中进行四次指数化，但仔细结合文献中的技巧（见 [56]），只需进行 3 次场指数化（都是 的幂），以及在 中进行少量的额外操作就可以实现对曲线的完整映射。辅因子的小标度乘法将这些哈希点移到大素阶子群内。

我们测量了我们的实现，从哈希到曲线的函数需要大约 12000 个时钟周期，标量乘法需要 42000 个时钟周期。这比 Aranha 和 Resende [54] 为不平衡 PSI 应用优化的曲线 GLS-254 快，后者的标量乘法需要大约 50，000 个时钟周期。

4 标签化 PSI

4.1 2018 年 Chen 等人的标签化 PSI

在有标签的 PSI 中，发送方为其每个项目 持有一个字节串 ，称为标签，长度为 。接收者为其每个项目 的交集学习相应的标签 。如 [13] 中所介绍的，其基本思路是由发送方构建插值多项式： 发送方对接收方的加密输入进行多项式评估，就像它评估相交多项式一样，并将结果发回给接收方。

剩下的就是构造多项式 ，然而，[13] 中的构造依赖于这样一个事实：内插是在扩展场上进行的，其中非零场元素可以通过与非零随机场元素相乘而被完全随机化。

4.2 改进措施

上述方法对我们的结构来说并不适用，因为我们把项目分成素字段元素大小的块，并对它们独立计算相交多项式。因此，一个部分匹配，由于素数域的大小很小，可能很容易被破解，会立即泄露标签的相应部分。

幸运的是，[13] 已经为这个问题提供了部分解决方案：由于我们在任何情况下都必须使用 ，我们可以扩展 的输出，并使用 值的一部分来代表相交多项式中的项目，另一部分作为对称密码的密钥来加密标签。然后，我们不对标签的部分内容进行插值，而是对加密的标签的部分内容进行插值（见图 2 的例子）。接收者在从该项目的完整 值中提取密钥后，将能够解密结果。这种技术确保只有知道交集中的项目的接收者才能解密与该项目对应的标签。

这种方法的一个主要缺点是场操作中插值的 复杂性。与 [13] 的扩展场相比，使用基元场会有很大的改进，但对于实际参数来说，成本仍然很高，令人遗憾。为了解决这个问题，我们注意到预计算是很容易更新的：项目可以被添加或删除，标签可以被更新。当对称密码是一个 流密码时，这就出现了一个问题：如果一个项目的标签被改变，而加密密钥和 nonce 保持不变，那么即使是一个半诚实的接收者也可以找到改变之前和之后的标签（或标签部分）的 。一个简单的解决方案是使用一个严格递增的 nonce 进行加密，但这在实践中是很难维护的。另一个解决方案是在每次更新时总是为每个标签选择一个随机的 nonce，并将其附加到标签数据的一部分。这样一来，接收者总是能得到正确的 nonce，并能用它来解密标签本身。在实践中，标签数据，特别是当附加了一个随机的 nonce 时，可能会比项目长。在这种情况下，标签数据被简单地分解成项目大小的片段，并为每个片段形成一个单独的插值多项式。然后，接收者将为每个片段获得一个单独的结果，重建加密的标签，并最终将其解密。

在 [13] 中指出，除了标签结果外，将交集结果返回给接收者严格来说是没有必要的，但在实践中可能需要接收者知道哪些标签值持有有效数据。因此，我们认为标签式 PSI 协议既要返回交集结果，又要返回一个或多个标签结果，这取决于标签是由单个还是多个项目长度的片段组成。

image-20220803215102266

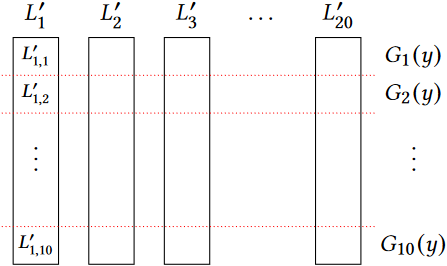
图 2：在这个例子中，有 个加密的标签 ，每个标签被分割成 个部分。红色的虚线表示不同的部分。为每个部分创建一个标签多项式 。

4.2.1 解决一个微妙的问题

不幸的是，上述方法还有一个技术问题需要解决。为了理解这个问题，请注意，[13] 在大的扩展字段上进行插值，其中一个扩展字段元素编码整个项目。由于项目从不重复，插值总是会成功。由于我们建议对标签的每个基元场大小的部分使用单独的插值多项式，插值是在一个小得多的场上进行的，在这里很容易出现项目部分的碰撞：一个分区（回顾第 3.1.2 节）可能会导致同一仓中出现重复的项目部分。如果相应的标签部分不匹配（很可能是这种情况），内插就不可能进行。

为了解决这个问题，发送者在插入一个项目时，必须检查它的任何部分是否已经出现在该项目被插入的分区的相同位置。如果遇到了碰撞，发送者必须尝试在不同的分区中插入该项目，或者作为最后的手段，创建一个全新的分区，在那里可以插入有问题的项目。

上述程序导致了一个不幸的现象，即与无标签的 PSI 相比，有标签的 PSI 会产生更多的分区，并且对发送方的数据结构的 "填充率" 更低。

4.2.2 安全性

虽然 [13] 没有明确讨论标记情况的安全证明，但我们注意到，理想功能（[13]，图 3）和非标记情况的安全证明（[13]，定理 1）可以直接扩展到标记情况。

在理想的功能中，发送方同时输入其集合 和一组标签 ，而接收方则学习 。扮演发送方的模拟器使用随机预言机从它的 查询中提取恶意接收方的输入 。然后将 交给理想函数，该函数以 进行响应。模拟器用随机 对将其填充到大小为 ，其中 和 ，用来自相应 值的密钥加密对应于接收器输入的标签值，并创建响应密文数据。该证明完全按照 [13] 的定理 1 完成。

5 实验

我们在两个 C++ 库中测试了上述技术，HElib [31] 和 SEAL [57]，它们分别实现了 BGV [7] 和 BFV [22] 方案。本节中使用的加密参数至少支持 128 位的安全性，除非另有标注（见表 5 和表 6）。基准测试是在 Intel Xeon Platinum 8272CL CPU @ 2.60 GHz 上进行的，有 24 个物理核心和 192GB 的内存。我们认为这与 [13] 中使用的 32 核机器相当。

两种实现方式的基本原理如下。SEAL 的实现有助于我们与先前的工作 [13, 14] 进行充分的比较。然而，SEAL 支持有限的加密参数集，阻碍了第 3.1 节中的低深度指数化技术 -- 我们降低通信成本的最有力工具。特别是，SEAL 中的环 的顺序是固定的，即 必须与 同调，大于或等于 的平方。明文模数的乘法阶数 必须相对较小，即 ，以允许以最大的 SIMD 容量对 80 位字符串进行编码。我们发现，在 [2, 3000] 范围内没有这样的素数 。对于更大的 ，低深度指数化技术在实践中几乎是无用的，因为 Frobenius 操作产生了一个非常稀疏的幂集。为了解决上述问题，我们求助于 HElib 库，其中的环状环 可以是任何阶数。

在基于 SEAL 的实现中，我们旨在展示我们的优化是如何比先前的工作，特别是 [13] 减少运行时间和通信成本的。这种设置利用了第 3.1 节的所有技术，除了低深度指数化方法。在 HElib 的实现中，我们只关注通信成本，并依赖于低深度指数化、SIMD 打包和 Paterson-Stockmeyer 方法。

与 SEAL 版本不同的是，HElib 版本是一个概念验证的实现，写它只是为了演示用于降低通信成本的低深度指数化技术。也就是说，我们没有实现 或网络。然而，我们能够准确地计算通信成本，因为 的成本是固定的（32 字节），在接收器的集合中的每一个项目和密码文本的大小可以在 HElib 中计算。我们在介绍中省略了 的计算成本（附录 D），因为它更难准确估计，我们的重点是通信成本。

我们的基于 SEAL 的协议是在一个开源的库中实现的，可在 https://GitHub.com/Microsoft/APSI 中找到。

5.1 基于 SEAL 的实现：无标签模式

表 1 给出了我们在无标签模式下运行的 SEAL 实现的计算和通信成本。对于每一对 ，我们只提出了一个结果，但实际上情况并不那么简单：协议涉及相当复杂的参数化，有许多通信 - 计算的权衡。我们提出的结果展示了我们认为最能体现整体性能的每种规模的问题的一个设置，但总是有可能通过增加通信来减少运行时间，反之亦然。

表 1 包括与 Chen 等人 [13] 的单线程执行的比较，包括发送方到接收方和接收方到发送方通信的细节。此外，在表 2 中，我们提出了另一个与 Chen 等人 [13]、Kales 等人 [36] 以及 Aranha 和 Resende [54] 的并列比较，这些协议代表了不平衡 PSI 的不同先进协议。

关于 Chen 等人 [13]，很明显，我们的协议在很多情况下更快，特别是对于较大的参数，并且在每一种情况下都有更小的通信成本。例如，对于 和 ，我们的计算 - 通信权衡使我们能够以在线计算的边际增加为代价减少 71% 的通信。我们的计算和通信成本大约是 [13] 中的三分之一。

我们的工作与 Kales 等人 [36] 之间的比较更加细微，因为协议和应用是不同的。对于协议方面，主要的区别是 Kales 等人有一个重要的发送方预处理步骤，并且需要一个可能很大的布谷鸟过滤器 提前从发送方传达给接收方，而我们的协议没有这种离线通信。另一方面，Kales 等人的计算成本在在线阶段以及预处理阶段更好，因为他们不需要进行任何昂贵的同态加密操作。在应用方面，Kales 等人 [36] 专注于移动联系人的发现，其中接收器是一个低功率的移动设备，但我们的协议并不针对具体的应用。由于这个原因，Kales 等人可能选择了需要更多在线通信的协议，例如，基于 的 ，以减少移动设备在在线阶段的计算成本。然而，我们想强调的是，我们在在线阶段的通信复杂度与 [36] 中的两个协议相当或好很多。

从表中无法看出的是，布谷鸟过滤器也导致 Kales 等人 [36] 有一个不可忽视的假阳性概率。在他们的实验中，他们将布谷鸟过滤器的参数化，使其假阳性概率为 。例如，如果 ，这导致接收器看到至少一个假阳性结果的概率约为 ，因此在不到 次调用中至少有一次调用协议会报告一个假阳性。虽然在某些应用中，这可能是可以接受的，但在其他应用中，这可能是不可接受的。另一方面，[13，14] 以及我们的变体，其假阳性概率最多只有 ，而且在实际实例中往往要小得多。

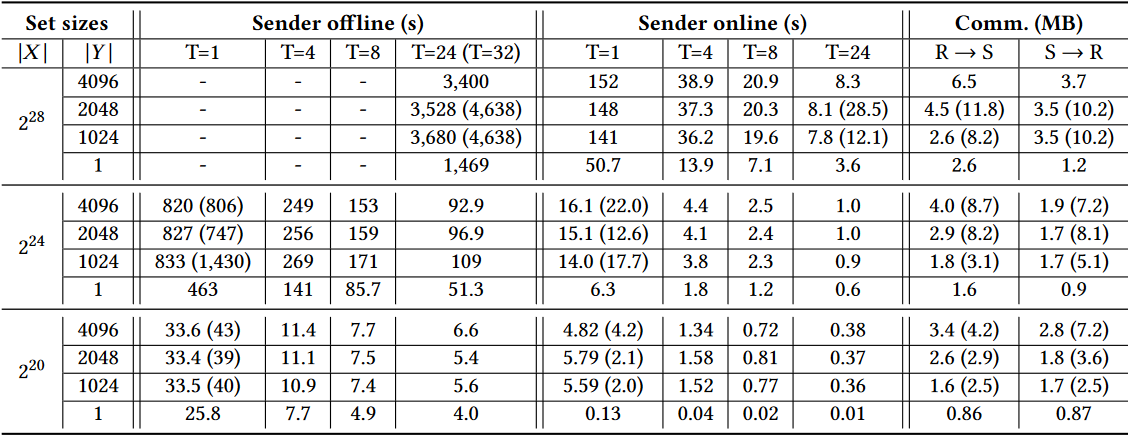
正如 Kales 等人 [36] 和 Chen 等人 [13] 一样，我们也包括与 Aranha 和 Resende [54] 的工作进行比较。然而，我们注意到 [54] 使用了极为激进的布谷鸟过滤器参数，导致在线性能远远优于其他协议，但假阳性率高达 ，这是不现实的。尽管有积极的布谷鸟过滤参数，[54] 在发送方集合很大的情况下，仍有离线通信复杂性高的问题。

image-20220803222559316

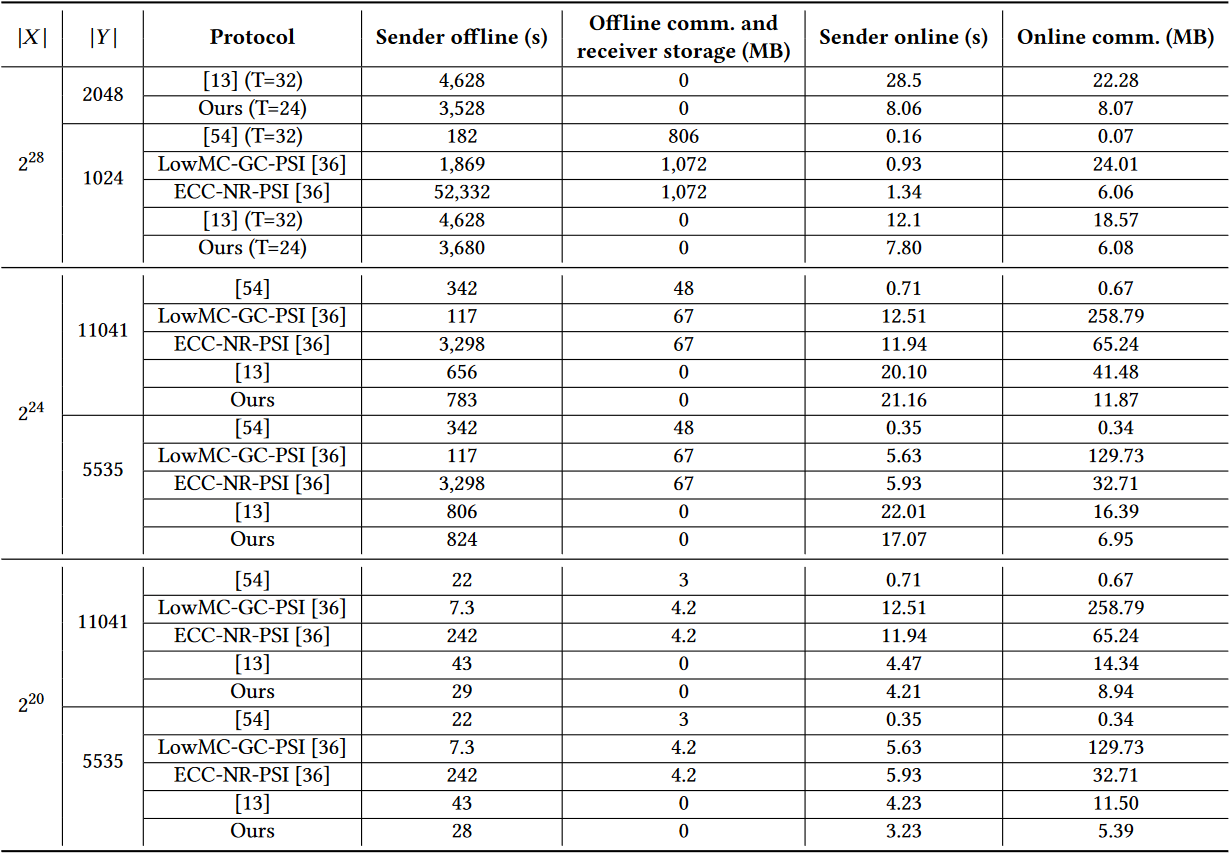
表 1：我们的 SEAL 实现的计算和通信成本。 表示线程数， 和 分别表示接收方到发送方和发送方到接收方的通信规模。时间是协议运行 10 次的平均数。Chen 等人 (CCS'18) 的单线程执行的相应数值在括号内，除了 的情况，Chen 等人 (CCS'18) 使用 32 个线程，我们与我们在 24 个线程上的执行进行比较。

image-20220803222617124

表 2：与先前工作的比较。所有的执行都是单线程的，除了那些线程数被明确标记为 等于线程数的。

5.2 非常大的发送者

Kales 等人 [36] 指出，在实际应用中，例如移动联系人的发现，遇到超过 10 亿的发送方集合是现实的。虽然我们的协议很容易扩展到这种情况，但在这么大的集合上运行我们的实现需要比我们的系统可用的内存多得多，从而导致大量的分页和在线计算的大量减慢。

因此，对于非常大的发送者来说，更可行的解决方案是将数据集划分为较小的部分，并以较小的参数多次运行该协议。我们注意到，接收方与发送方之间的通信只需要做一次，因此，例如对一个 的发送方运行我们的协议，只需要 的通信， ，而 [36] 则需要从发送方到接收方进行大约 的布谷鸟过滤器通信，这显然是不现实的。

5.3 基于 SEAL 的实现：标签化模式

我们也在标签模式下演示几个例子。标签的大小很重要，即回顾一下第 4.2 节，如果标签比项目长度（更正确地说，是用来表示项目的 值的长度）长，那么标签必须被分解成多个项目长度的块，必须形成单独的插值多项式，然后对每个块进行评估。由于相同的加密查询数据被用于评估每个块的插值多项式，标签的大小对接收方到发送方的通信没有直接影响。然而，发送方到接收方的通信量随着块的数量而线性增加。因此，如果标签很长，以增加接收方之间通信的代价，将协议参数化，使发送方 - 接收方的通信最小化是有益的。

不幸的是，并没有很多有意义的比较点。Chen 等人 [13] 提出了一个与 PIR 论文 [3] 进行比较的单一数据点，其中标签大小为 ，我们使用我们的优化措施复制了这个实验；结果见表 3。我们的协议在所有测量方面都明显优于这两点的比较。更多关于标签大小 和 的例子见表 4。

image-20220803222810112

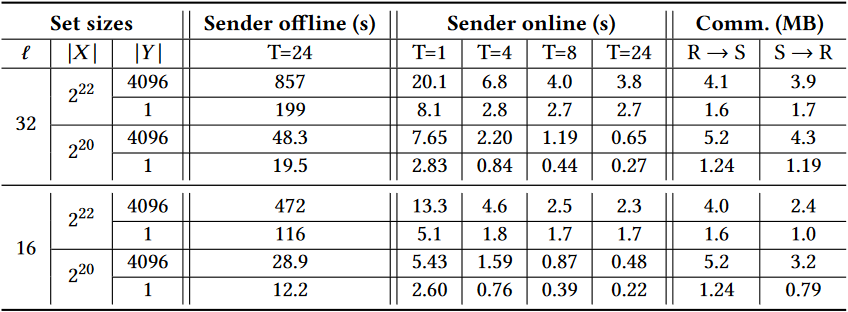
表 3：在标签字节长度 的标签模式下与先前的工作比较。发送方使用 16 个线程，接收方使用一个线程。

image-20220803222830938

表 4：我们的 SEAL 实现在标签设置中的计算和通信成本。标签的字节大小为 ，而线程的数量用 表示，时间是协议运行 10 次的平均值。

5.4 基于 HElib 的实现：对通信复杂性进行优化

我们在 HElib 中的概念验证实现，旨在说明非平衡 PSI 可以在 中实现亚对数的通信复杂度。我们用含有任意比特长度元素的 和 进行了实验。这些元素在协议的布谷鸟散列阶段被散列成 位字符串。发送方的集合大小为 ，接收方的集合大小为 。为了得到尽可能小的通信成本，我们避免分区（即我们取 ）。既没有利用窗口法，也没有利用极值邮票基。

如第 3.1.6 节所述，在执行我们的 PSI 协议之前，接收方会向发送方发送 评估密钥。密钥的数量可以减少到一个，但要付出额外的 Frobenius 操作。由于评估密钥与 无关，它们可以只发送一次，并为协议的重复执行进行缓存。因此，表 5 的通信开销可以在多个接收者的请求中摊销。

我们的 PSI 协议的通信费用显示在表 6 中。为了比较，我们还包括了 [13] 的通信成本。请注意，在 [13] 中，评估密钥和密码文本是在对称密钥模式下生成的，这使得我们可以将其大小几乎减半。不幸的是，我们无法在 HElib 中使用这种模式，但我们向 [13] 作者索取了公钥模式下的相应通信量。

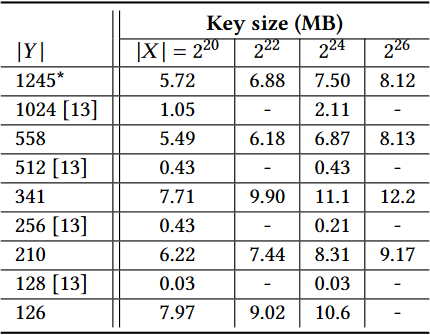
如表 6 所示，我们的实现的通信成本随着发送方集合的大小增长非常缓慢。例如，对于 从 到 ，它保持不变。此外，在我们测试的所有参数中，发送方集的 倍增长导致通信规模增加 6-20%。与 [13] 相比，这是一个小得多的增长，在 [13] 中， 倍的增加 导致通信量上升 40-291%。更多的结果与相应的加密参数和运行时间可以在附录 D 中找到。

image-20220803222944740

表 5：我们的 HElib 实现和先前工作 [13] 在离线阶段的评估密钥大小。在这些实验中使用的所有参数的安全级别至少是 位，除了带 的参数，它至少是 位。

image-20220803222954775

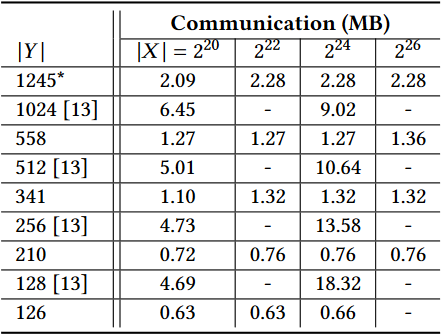
表 6：我们的 HElib 实现和先前工作 [13] 在在线阶段的通信成本。在这些实验中使用的所有参数的安全级别至少是 位，除了带 的参数，它至少是 位。

6 结论

我们已经证明了对 [13] 协议的一些改进，大大降低了通信和在线计算成本。我们的改进实现了非常强大的通信计算权衡，可以利用这些权衡使该协议在各种情况下都是实用的和可扩展的。最后，我们表明，同态加密可以用来在不平衡的情况下实现 PSI，在较大的集合中具有亚对数的通信成本，尽管这个协议现在还不实用。在未来，对同态加密的硬件加速可能会改变这种情况。

鸣谢

我们要感谢 Craig Costello 和 Patrick Longa（微软研究院）在 FourQ 曲线的 hash-tocurve 算法方面提供的重要帮助和建议，以及对 FourQlib 库的支持，还要感谢陈浩（Facebook）在这项工作的初步阶段进行的有益讨论。

这项工作得到了 CyberSecurity Research Flanders 的支持，参考编号为 VR20192203。此外，第一作者得到了美国国防部高级研究计划局（DARPA）和太平洋空间和海军作战系统中心（SSC Pacific）的支持，合同号为 FA8750-19-C-0502。第三位作者得到 ERC 高级拨款 ERC-2015-AdG-IMPaCT 和佛兰德政府通过 FWO SBO 项目 SNIPPET S007619N 的支持。第五位作者得到法兰德斯研究基金会（FWO）的初级博士后研究金的支持。

本材料中表达的任何意见、发现和结论或建议都是作者的观点，不一定反映佛兰德斯网络安全研究中心、DARPA、美国政府、ERC 或 FWO 的观点。美国政府被授权为政府目的而复制和分发重印本，尽管其中有任何版权注释。

最后，我们要感谢匿名审稿人的有益意见。

参考文献

  1. Martin R. Albrecht, Rachel Player, and Sam Scott. 2015. On the concrete hardness of Learning with Errors. J. Mathematical Cryptology 9, 3 (2015), 169203. http://www.degruyter.com/view/j/jmc.2015.9.issue-3/jmc-2015-0016/jmc2015- 0016.xml

  2. Junade Ali. 2018. Validating Leaked Passwords with k-Anonymity. https://blog. cloudflare.com/validating-leaked-passwords-with-k-anonymity/. Accessed: 2021-04-26.

  3. Sebastian Angel, Hao Chen, Kim Laine, and Srinath Setty. 2018. PIR with compressed queries and amortized query processing. In 2018 IEEE Symposium on Security and Privacy (SP). IEEE, 962–979.

  4. Giuseppe Ateniese, Emiliano De Cristofaro, and Gene Tsudik. 2011. (If) Size Matters: Size-Hiding Private Set Intersection. In PKC 2011 (LNCS, Vol. 6571), Dario Catalano, Nelly Fazio, Rosario Gennaro, and Antonio Nicolosi (Eds.). Springer, Heidelberg, 156–173. https://doi.org/10.1007/978-3-642-19379-8_10

  5. Daniel J Bernstein, Mike Hamburg, Anna Krasnova, and Tanja Lange. 2013. Elligator: Elliptic-curve points indistinguishable from uniform random strings. In Proceedings of the 2013 ACM SIGSAC conference on Computer & communications security. 967–980.

  6. Zvika Brakerski. 2012. Fully Homomorphic Encryption without Modulus Switching from Classical GapSVP. In CRYPTO (Lecture Notes in Computer Science, Vol. 7417), Reihaneh Safavi-Naini and Ran Canetti (Eds.). Springer, 868–886.

  7. Zvika Brakerski, Craig Gentry, and Vinod Vaikuntanathan. 2012. (Leveled) fully homomorphic encryption without bootstrapping. In Proceedings of the 3rd Innovations in Theoretical Computer Science Conference. ACM, 309–325.

  8. Zvika Brakerski and Vinod Vaikuntanathan. 2011. Fully homomorphic encryption from ring-LWE and security for key dependent messages. In Advances in Cryptology–CRYPTO 2011. Springer, 505–524.

  9. Zvika Brakerski and Vinod Vaikuntanathan. 2014. Efficient fully homomorphic encryption from (standard) LWE. SIAM J. Comput. 43, 2 (2014), 831–871.

  10. Michael F. Challis. 1993. Two new techniques for computing extremal h-bases Ak. Comput. J. 36, 2 (1993), 117–126.

  11. Michael F Challis and John P Robinson. 2010. Some extremal postage stamp bases. Journal of Integer Sequences 13, 2 (2010), 3.

  12. Melissa Chase and Peihan Miao. 2020. Private Set Intersection in the Internet Setting from Lightweight Oblivious PRF. In CRYPTO 2020, Part III (LNCS), Hovav Shacham and Alexandra Boldyreva (Eds.). Springer, Heidelberg, 34–63.

  13. Hao Chen, Zhicong Huang, Kim Laine, and Peter Rindal. 2018. Labeled PSI from Fully Homomorphic Encryption with Malicious Security. In ACM CCS 2018, David Lie, Mohammad Mannan, Michael Backes, and XiaoFeng Wang (Eds.). ACM Press, 1223–1237. https://doi.org/10.1145/3243734.3243836

  14. Hao Chen, Kim Laine, and Peter Rindal. 2017. Fast Private Set Intersection from Homomorphic Encryption. In ACM CCS 2017, Bhavani M. Thuraisingham, David Evans, Tal Malkin, and Dongyan Xu (Eds.). ACM Press, 1243–1255. https://doi.org/10.1145/3133956.3134061

  15. Ilaria Chillotti, Nicolas Gama, Mariya Georgieva, and Malika Izabachene. 2016. Faster fully homomorphic encryption: Bootstrapping in less than 0.1 seconds. In International Conference on the Theory and Application of Cryptology and Information Security. Springer, 3–33.

  16. Benny Chor, Niv Gilboa, and Moni Naor. 1997. Private information retrieval by keywords. Citeseer.

  17. Craig Costello and Patrick Longa. 2015. FourQ: four-dimensional decompositions on a Q-curve over the Mersenne prime. Cryptology ePrint Archive, Report 2015/565. https://eprint.iacr.org/2015/565.

  18. Whitfield Diffie and Martin E. Hellman. 1976. New Directions in Cryptography. IEEE Transactions on Information Theory 22, 6 (1976), 644–654.

  19. Changyu Dong, Liqun Chen, and Zikai Wen. 2013. When private set intersection meets big data: an efficient and scalable protocol. In ACM CCS 2013, Ahmad-Reza Sadeghi, Virgil D. Gligor, and Moti Yung (Eds.). ACM Press, 789–800. https: //doi.org/10.1145/2508859.2516701

  20. Léo Ducas and Daniele Micciancio. 2015. FHEW: Bootstrapping Homomorphic Encryption in Less Than a Second. In EUROCRYPT 2015, Part I (LNCS, Vol. 9056), Elisabeth Oswald and Marc Fischlin (Eds.). Springer, Heidelberg, 617–640.

  21. Bin Fan, Dave G. Andersen, Michael Kaminsky, and Michael D. Mitzenmacher. 2014. Cuckoo Filter: Practically Better Than Bloom. In Proceedings of the 10th ACM International on Conference on Emerging Networking Experiments and Technologies (Sydney, Australia) (CoNEXT ’14). Association for Computing Machinery, New York, NY, USA, 75–88. https://doi.org/10.1145/2674005.2674994

  22. Junfeng Fan and Frederik Vercauteren. 2012. Somewhat Practical Fully Homomorphic Encryption. Cryptology ePrint Archive, Report 2012/144. http: //eprint.iacr.org/.

  23. Michael J. Freedman, Yuval Ishai, Benny Pinkas, and Omer Reingold. 2005. Keyword Search and Oblivious Pseudorandom Functions. In TCC 2005 (LNCS, Vol. 3378), Joe Kilian (Ed.). Springer, Heidelberg, 303–324.

  24. Michael J. Freedman, Kobbi Nissim, and Benny Pinkas. 2004. Efficient Private Matching and Set Intersection. In EUROCRYPT 2004 (LNCS, Vol. 3027), Christian Cachin and Jan Camenisch (Eds.). Springer, Heidelberg, 1–19. https://doi.org/10. 1007/978- 3- 540- 24676- 3_1

  25. Craig Gentry. 2009. Fully homomorphic encryption using ideal lattices.. In STOC, Vol. 9. 169–178.

  26. Craig Gentry, Shai Halevi, and Nigel P Smart. 2012. Homomorphic evaluation of the AES circuit. In Advances in Cryptology–CRYPTO 2012. Springer, 850–867.

  27. Craig Gentry, Amit Sahai, and Brent Waters. 2013. Homomorphic Encryption from Learning with Errors: Conceptually-Simpler, Asymptotically-Faster, Attribute-Based. In CRYPTO (1) (Lecture Notes in Computer Science, Vol. 8042), Ran Canetti and Juan A. Garay (Eds.). Springer, 75–92. https://doi.org/10.1007/9783- 642- 40041- 4

  28. Christoph Hagen, Christian Weinert, Christoph Sendner, Alexandra Dmitrienko, and Thomas Schneider. 2021. All the Numbers are US: Large-scale Abuse of Contact Discovery in Mobile Messengers. In 28th Annual Network and Distributed System Security Symposium, NDSS. The Internet Society.

  29. Shai Halevi and Victor Shoup. 2020. Design and implementation of HElib: a homomorphic encryption library. Cryptology ePrint Archive, Report 2020/1481. https://eprint.iacr.org/2020/1481.

  30. Carmit Hazay and Yehuda Lindell. 2008. Efficient Protocols for Set Intersection and Pattern Matching with Security Against Malicious and Covert Adversaries. In Theory of Cryptography, Ran Canetti (Ed.). Springer Berlin Heidelberg, Berlin, Heidelberg, 155–175.

  31. HElib 2021. HElib: An Implementation of homomorphic encryption (2.1.0). https://github.com/homenc/HElib. IBM.

  32. Yan Huang, David Evans, and Jonathan Katz. 2012. Private Set Intersection: Are Garbled Circuits Better than Custom Protocols?. In NDSS 2012. The Internet Society.

  33. Bernardo A. Huberman, Matt Franklin, and Tad Hogg. 1999. Enhancing Privacy and Trust in Electronic Communities. In Proceedings of the 1st ACM Conference on Electronic Commerce (Denver, Colorado, USA) (EC ’99). Association for Computing Machinery, New York, NY, USA, 78–86. https://doi.org/10.1145/336992.337012

  34. Yuval Ishai, Joe Kilian, Kobbi Nissim, and Erez Petrank. 2003. Extending Oblivious Transfers Efficiently. In CRYPTO 2003 (LNCS, Vol. 2729), Dan Boneh (Ed.). Springer, Heidelberg, 145–161. https://doi.org/10.1007/978-3-540-45146-4_9

  35. Stanisław Jarecki and Xiaomin Liu. 2010. Fast secure computation of set intersection. In International Conference on Security and Cryptography for Networks. Springer, 418–435.

  36. Daniel Kales, Christian Rechberger, Thomas Schneider, Matthias Senker, and Christian Weinert. 2019. Mobile Private Contact Discovery at Scale. In USENIX Security 2019, Nadia Heninger and Patrick Traynor (Eds.). USENIX Association, 1447–1464.

  37. Sreekanth Kannepalli, Kim Laine, and Radames Cruz Moreno. 2021. Password Monitor: Safeguarding passwords in Microsoft Edge. https: //www.microsoft.com/en- us/research/blog/password- monitor- safeguardingpasswords-in-microsoft-edge/. Accessed: 2021-04-26.

  38. Andrey Kim, Yuriy Polyakov, and Vincent Zucca. 2021. Revisiting Homomorphic Encryption Schemes for Finite Fields. Cryptology ePrint Archive, Report 2021/204. https://eprint.iacr.org/2021/204.

  39. Ágnes Kiss, Jian Liu, Thomas Schneider, N. Asokan, and Benny Pinkas. 2017. Private Set Intersection for Unequal Set Sizes with Mobile Applications. PoPETs 2017, 4 (Oct. 2017), 177–197. https://doi.org/10.1515/popets-2017-0044

  40. Vladimir Kolesnikov, Ranjit Kumaresan, Mike Rosulek, and Ni Trieu. 2016. Efficient Batched Oblivious PRF with Applications to Private Set Intersection. In ACM CCS 2016, Edgar R. Weippl, Stefan Katzenbeisser, Christopher Kruegel, Andrew C. Myers, and Shai Halevi (Eds.). ACM Press, 818–829. https://doi.org/ 10.1145/2976749.2978381

  41. Vadim Lyubashevsky, Chris Peikert, and Oded Regev. 2013. On ideal lattices and learning with errors over rings. Journal of the ACM (JACM) 60, 6 (2013), 43.

  42. Moxie Marlinspike. 2014. The Difficulty Of Private Contact Discovery. A company sponsored blog post. https://signal.org/blog/contact-discovery/.

  43. C. Meadows. 1986. A More Efficient Cryptographic Matchmaking Protocol for Use in the Absence of a Continuously Available Third Party. In 1986 IEEE Symposium on Security and Privacy. 134–134. https://doi.org/10.1109/SP.1986.10022

  44. Moni Naor and Omer Reingold. 2004. Number-theoretic constructions of efficient pseudo-random functions. Journal of the ACM 51, 2 (2004), 231–262.

  45. Andrew Odlyzko. 2003. Privacy, economics, and price discrimination on the Internet. In Proceedings of the 5th international conference on Electronic commerce. ACM, 355–366.

  46. Michele Orrù, Emmanuela Orsini, and Peter Scholl. 2017. Actively Secure 1-outof-N OT Extension with Application to Private Set Intersection. In CT-RSA 2017 (LNCS, Vol. 10159), Helena Handschuh (Ed.). Springer, Heidelberg, 381–396. https: //doi.org/10.1007/978- 3- 319- 52153- 4_22

  47. Michael S Paterson and Larry J Stockmeyer. 1973. On the number of nonscalar multiplications necessary to evaluate polynomials. SIAM J. Comput. 2, 1 (1973), 60–66.

  48. Benny Pinkas, Mike Rosulek, Ni Trieu, and Avishay Yanai. 2020. PSI from PaXoS: Fast, Malicious Private Set Intersection. In EUROCRYPT 2020, Part II (LNCS), Vincent Rijmen and Yuval Ishai (Eds.). Springer, Heidelberg, 739–767.

  49. Benny Pinkas, Thomas Schneider, Gil Segev, and Michael Zohner. 2015. Phasing: Private set intersection using permutation-based hashing. In 24th USENIX Security Symposium (USENIX Security 15). 515–530.

  50. Benny Pinkas, Thomas Schneider, Nigel P. Smart, and Stephen C. Williams. 2009. Secure Two-Party Computation Is Practical. In ASIACRYPT 2009 (LNCS, Vol. 5912), Mitsuru Matsui (Ed.). Springer, Heidelberg, 250–267.

  51. Benny Pinkas, Thomas Schneider, Christian Weinert, and Udi Wieder. 2018. Efficient Circuit-Based PSI via Cuckoo Hashing. In EUROCRYPT 2018, Part III (LNCS, Vol. 10822), Jesper Buus Nielsen and Vincent Rijmen (Eds.). Springer, Heidelberg, 125–157. https://doi.org/10.1007/978-3-319-78372-7_5

  52. Benny Pinkas, Thomas Schneider, and Michael Zohner. 2014. Faster Private Set Intersection Based on OT Extension. In USENIX Security 2014, Kevin Fu and Jaeyeon Jung (Eds.). USENIX Association, 797–812.

  53. Oded Regev. 2005. On lattices, learning with errors, random linear codes, and cryptography. In Proceedings of the 37th Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, May 22-24, 2005, Harold N. Gabow and Ronald Fagin (Eds.). ACM, 84–93. https://doi.org/10.1145/1060590.1060603

  54. Amanda C. Davi Resende and Diego F. Aranha. 2018. Faster Unbalanced Private Set Intersection. In FC 2018 (LNCS, Vol. 10957), Sarah Meiklejohn and Kazue Sako (Eds.). Springer, Heidelberg, 203–221.

  55. Peter Rindal and Mike Rosulek. 2017. Malicious-Secure Private Set Intersection via Dual Execution. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security (Dallas, Texas, USA) (CCS ’17). ACM, New York, NY, USA, 1229–1242. https://doi.org/10.1145/3133956.3134044

  56. Michael Scott. 2020. A note on the calculation of some functions in finite fields: Tricks of the Trade. Cryptology ePrint Archive, Report 2020/1497. https: //eprint.iacr.org/2020/1497.

  57. SEAL 2020. Microsoft SEAL (release 3.6). https://github.com/Microsoft/SEAL. Microsoft Research, Redmond, WA..

  58. Victor Shoup. 2021. NTL: A Library for doing Number Theory (11.4.3). https: //libntl.org/.

  59. Nigel P Smart and Frederik Vercauteren. 2014. Fully homomorphic SIMD operations. Designs, codes and cryptography 71, 1 (2014), 57–81.

  60. Ni Trieu, Kareem Shehata, Prateek Saxena, Reza Shokri, and Dawn Song. 2020. Epione: Lightweight contact tracing with strong privacy.

  61. Andrew Chi-Chih Yao. 1986. How to Generate and Exchange Secrets (Extended Abstract). In 27th FOCS. IEEE Computer Society Press, 162–167. https://doi.org/ 10.1109/SFCS.1986.25

A 分区的 Paterson-Stockmeyer 算法的复杂性

B 例证 2 的证明

C 例证 5 的证明

D 在 HELIB 的实验结果